Критерий Манна-Уитни
. Литература. Mann H.
B., Whitney D. On a test of whether one of two random variables is stochastically larger than the other. // Annals of Mathematical Statistics. — 1947. — № 18. — P. Wilcoxon F. Individual Comparisons by Ranking Methods. // Biometrics Bulletin 1. — 1945. — P.
Критерий Манна-Уитни применяют для оценки различий по уровню выраженности того или иного. U-критерий Манна-Уитни - непараметрический метод проверки гипотез, часто использующийся в качестве альтернативы t-тесту Стьюдента. Обычно этот тест используется для сравнения медиан двух распределений X и Y, не являющихся нормальными (отсутствие нормальности не позволяет применить.
В., Генкин А. Применение непараметрических критериев статистики в медико-биологических исследованиях. — Л., 1973. Сидоренко Е. Методы математической обработки в психологии. — С-Пб., 2002.
Содержание. История Данный метод выявления различий между выборками был предложен в году Френком Уилкоксоном (F. В году он был существенно переработан и расширен Х.
Whitney), по именам которых сегодня обычно и называется. Описание критерия Простой непараметрический критерий. Мощность критерия выше, чем. Этот метод определяет, достаточно ли мала зона перекрещивающихся значений между двумя рядами (ранжированным рядом значений параметра в первой выборке и таким же во второй выборке). Чем меньше значение критерия, тем вероятнее, что различия между значениями параметра в выборках достоверны. Ограничения применимости критерия.
В каждой из выборок должно быть не менее 3 значений признака. Допускается, чтобы в одной выборке было два значения, но во второй тогда не менее пяти. В выборочных данных не должно быть совпадающих значений (все числа - разные) или таких совпадений должно быть очень мало. Использование критерия Для применения U-критерия Манна-Уитни нужно произвести следующие операции. Составить единый ранжированный ряд из обеих сопоставляемых выборок, расставив их элементы по степени нарастания признака и приписав меньшему значению меньший ранг. Общее количество рангов получится равным: N = n 1 + n 2, где n 1 — количество единиц в первой выборке, а n 2 — количество единиц во второй выборке. Разделить единый ранжированный ряд на два, состоящие соответственно из единиц первой и второй выборок.
Подсчитать отдельно сумму рангов, пришедшихся на долю элементов первой выборки, и отдельно — на долю элементов второй выборки. Определить большую из двух ранговых сумм ( T x), соответствующую выборке с n x единиц. Определить значение U-критерия Манна-Уитни по формуле:.

По таблице для избранного уровня статистической значимости определить критическое значение критерия для данных n 1 и n 2. Если полученное значение U меньше табличного или равно ему, то признается наличие существенного различия между уровнем признака в рассматриваемых выборках (принимается альтернативная гипотеза). Если же полученное значение U больше табличного, принимается. Достоверность различий тем выше, чем меньше значение U. При справедливости нулевой гипотезы критерий имеет матожидание и дисперсию и при достаточно большом объёме выборочных данных ( n 1 19, n 2 19) распределён практически нормально.
Таблица критических значений. Литература. Русский язык в упражнениях хавронина широченская. Mann H.B., Whitney D.R. On a test of whether one of two random variables is stochastically larger than the other. // Annals of Mathematical Statistics. Wilcoxon F.
Individual Comparisons by Ranking Methods. // Biometrics Bulletin 1. Гублер Е.В., Генкин А.А. Применение непараметрических критериев статистики в медико-биологических исследованиях. Сидоренко Е.В. Методы математической обработки в психологии.
Wikimedia Foundation. Смотреть что такое 'U-критерий Манна-Уитни' в других словарях:. — — media.ru/glossary/index.html?glossid=2400324 Тематики электросвязь, основные понятия EN Mann Whitney U test Справочник технического переводчика. — U критерий Манна Уитни (англ. Mann Whitney U test) непараметрический статистический критерий, используемый для оценки различий между двумя выборками по уровню какого либо признака, измеренного количественно. Позволяет выявлять различия в значении Википедия. — U критерий Манна Уитни (англ.
Mann Whitney U test) непараметрический статистический критерий, используемый для оценки различий между двумя выборками по уровню какого либо признака, измеренного количественно. Позволяет выявлять различия в значении Википедия. Biss ключи на ямал,abs. — U критерий Манна Уитни (англ. Mann Whitney U test) непараметрический статистический критерий, используемый для оценки различий между двумя выборками по уровню какого либо признака, измеренного количественно. Позволяет выявлять различия в значении Википедия. — U критерий Манна Уитни (англ.
Mann Whitney U test) статистический критерий, используемый для оценки различий между двумя выборками по уровню какого либо признака, измеренного количественно. Позволяет выявлять различия в значении Википедия. — U критерий Манна Уитни (англ.
Mann Whitney U test) непараметрический статистический критерий, используемый для оценки различий между двумя выборками по уровню какого либо признака, измеренного количественно. Позволяет выявлять различия в значении Википедия. — U критерий Манна Уитни (англ. Mann Whitney U test) непараметрический статистический критерий, используемый для оценки различий между двумя выборками по уровню какого либо признака, измеренного количественно. Позволяет выявлять различия в значении Википедия. — критерий для проверки гипотезы Н 0 об однородности двух выборок X1., Х п и Y1., Y т, все п+т элементов к рых взаимно независимы и подчиняются непрерывным распределениям. Этот критерий, предложенный X.
Уитни 1, построен на Математическая энциклопедия. — U критерий Манна Уитни (англ. Mann Whitney U test) статистический критерий, используемый для оценки различий между двумя независимыми выборками по уровню какого либо признака, измеренного количественно. Позволяет выявлять Википедия.
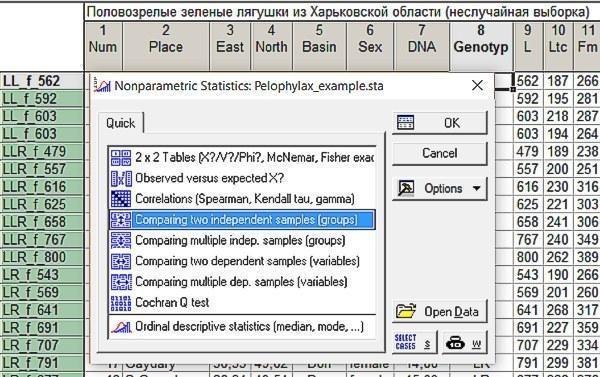
Критерий Манна-уитни Онлайн
— или Критерий согласия Колмогорова Смирнова статистический критерий, использующийся для определения того, подчиняются ли два эмпирических распределения одному закону, либо того, подчиняется ли полученное распределение предполагаемой модели.
